Logistics:

Credits:	4
Classes:	Tuesdays and Thursdays, 4:40pm to 6:10pm
Classsroom:	AC-02-LR-213
Instructor Office Hours:	Fridays, 3:00pm to 5:00pm at AC04-705
Teaching Assistant:	Elvia Dey (elvia.dey_asp25@ashoka.edu.in)
Instructor Office Hours:	Thursdays, 2:30pm to 3:30pm at AC04-736

Links:

Course Outline and Lectures

Course Project Guidelines

Scribing Guidelines

Resources and Reading Materials

Feedback, Appraisals, and Reflection

A Limerick

Course Description: Symbolic logic presents an intriguing challenge in computer science: balancing the need to express complex ideas with the ability to solve problems efficiently. This course explores how we can create systems that are powerful enough to describe useful scenarios, yet still allow computers to reason about them effectively. We'll examine various approaches to this balance, learning how theorists and practitioners have developed ways to represent knowledge and automate reasoning. Without requiring any prior background in logic or advanced mathematics, this course offers a gentle yet rigorous introduction to deductive systems, propositional and predicate calculi, and higher-order logic. We will also learn about the applications of these formalisms to constraint solving, program verification, automated reasoning, and interactive theorem proving. The objectives of this course are to:

1. Develop a foundation in the core concepts and deductive systems of propositional logic, predicate logic, and higher-order logics, including their syntax, semantics, and proof techniques,
2. Gain knowledge of the practical applications of symbolic logic in a variety of domains, such as constraint solving, program verification, automated reasoning, and interactive theorem proving,
3. Understand the trade-off between expressiveness and algorithmic tractability in logical formalisms, and the importance of finding reasonable compromises between these conflicting goals,
4. Understand the fundamental limitations of formal logic, reasoning, and computation, and
5. Develop hands-on experience working with tools like SAT solvers and interactive theorem provers, bridging the gap between theoretical reasoning and practical considerations.
   

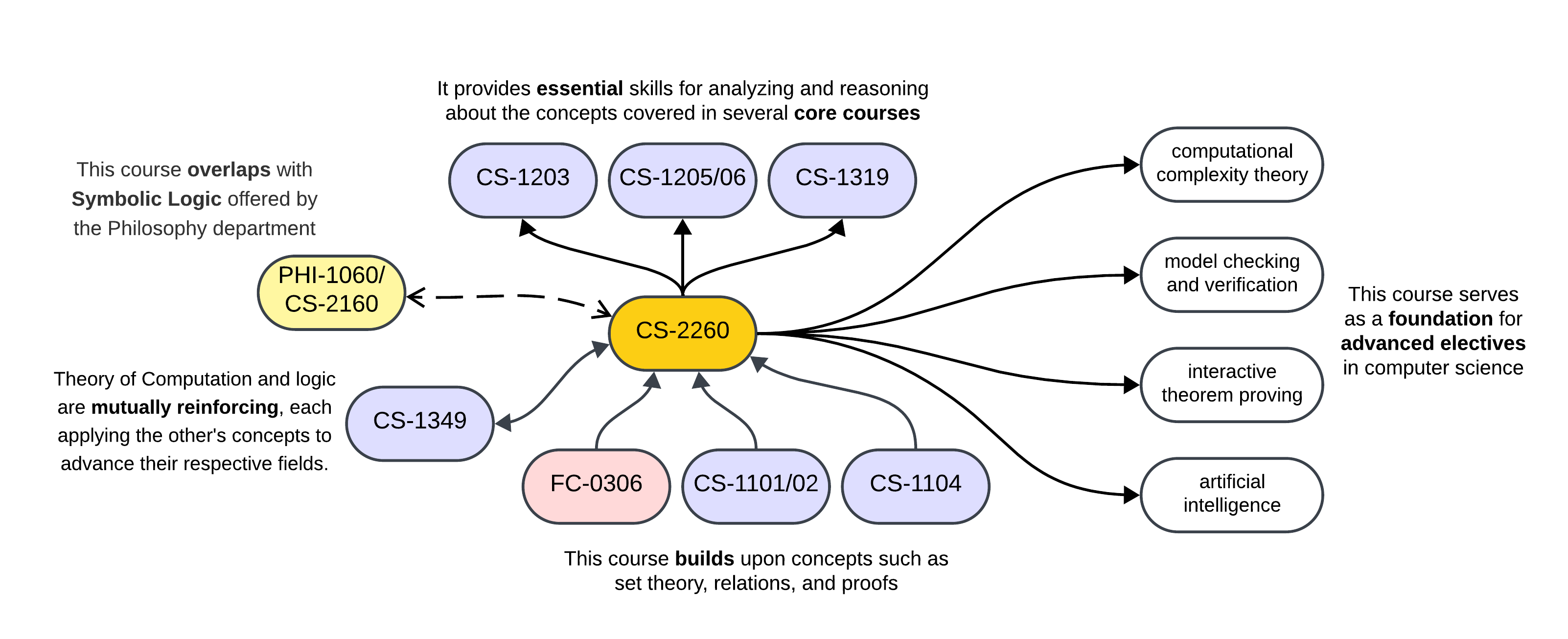
This course builds upon concepts such as set theory, relations, and proofs covered in Quantitative Reasoning and Mathematical Thinking (FC-0306), Introduction to Computer Science (CS-1101/1102), and Discrete Mathematics (CS-1104). It also provides essential skills for analyzing and reasoning about the concepts covered in Data Structures (CS-1203), Design and Analysis of Algorithms (CS-1205/1206), Theory of Computation (CS-1349/2349) Programming Language Design and Implementation (CS-1319). This course serves as a foundation for advanced electives in computer science including interactive theorem proving, model checking and verification, computational complexity theory, and Artificial Intelligence (CS-2322). This course overlaps with Symbolic Logic (PHI-1060/CS-2160).

Prerequisites: First, the course will require a certain amount of mathematical maturity at least at the level of FC-0306, and preferably at the level of CS-1101/02. Second, functional knowledge of a programming language (preferably Python) is required for completing the assignments and projects in this course.

Grading: A serious student of a subject is not an idle spectator to a variety show but learns best by active involvement. This is particularly true of mathematical subjects. This course is structured to incentivise involvement through the following:

1. Scribing: Each student will be responsible for taking detailed notes during the lectures assigned to them and drafting them in LaTeX. This exercise encourages active listening and helps consolidate understanding of the material. It constitutes 10% of the grade.
2. Course Project: Students will undertake a project on constraint solving (which requires programming). This hands-on experience allows for practical application of course concepts and fosters deeper engagement with the subject matter covered in Module 3. The project may be done either alone or in pairs. Project topic needs to be approved by the instructor. It carries 20% of the grade.
3. Assignments: The course includes 10 problem sets. These are designed to reinforce lecture material and develop practical skills in applying theoretical concepts. They constitute 40% of the grade.
4. Examination: Two in-class, closed-book, 1.5 hour examinations carry the remaining 30% of the grade. Students are permitted to bring a single, two-sided "cheat sheet" of their own creation.

Assignments: Assignments will be available every Tuesday after class and will be due by 9am the following Monday. We aim to grade assignments in the same week. Please use turnitin.com to submit assignments. No extensions will be granted except in the case of medical emergencies, proof of which must be emailed to the teaching assistant within 24 hours of the request.

Audit Requirements: The audit grade for this course will be evaluated based only on assignments and projects (students must complete at least 6 of the 10 assignments). Students auditing the course need not take the exams or meet the scribing requirements. Students are welcome to audit this course without a grade.

Policies: Students are expected to review and abide by Ashoka's Academic Integrity Policy (MyAshoka → Information and Documents → Office of Academic Affairs). Attendance is not mandated for this course, with two exceptions: (1) Each student will be assigned to scribe for one or more classes; attendance is required for the assigned classes. (2) All students are required to attend and actively participate in the discussion during Lecture 11 (October 1) and Course Project Presentations (November 28).

Support: Students are encouraged to reach out to University offices such as the Office of Learning Support, Ashoka Center for Well-Being, and Center for Writing and Communication for additional support.

Calendar:

Sunday	Monday	Tuesday	Wednesday	Thursday	Friday	Saturday
Aug 25	Aug 26	Aug 27 Lecture 1	Aug 28	Aug 29 Lecture 2	Aug 30 Office Hours	Aug 31
Sep 1	Sep 2	Sep 3 Lecture 3 Assignment 1	Sep 4	Sep 5 Lecture 4 Office Hours	Sep 6	Sep 7
Sep 8	Sep 9 Assignment 1 Due	Sep 10 Lecture 5 Assignment 2	Sep 11	Sep 12 Lecture 6	Sep 13 Office Hours	Sep 14
Sep 15	Sep 16 Assignment 2 Due†	Sep 17 Lecture 7 Assignment 3	Sep 18	Sep 19 Lecture 8	Sep 20 Office Hours	Sep 21
Sep 22	Sep 23	Sep 24 Lecture 9 Assignment 4	Sep 25 Assignment 3 Due	Sep 26 Lecture 10	Sep 27 Office Hours	Sep 28 Project Proposal Appraisal I
Sep 29	Sep 30 Assignment 4 Due	Oct 1 Lecture 11*	Oct 2 Office Hours	Oct 3 Mid-term Exam	Oct 4	Oct 5
Oct 6	Oct 7	Oct 8	Oct 9	Oct 10	Oct 11	Oct 12
Oct 13	Oct 14	Oct 15 Lecture 12 Assignment 5	Oct 16	Oct 17	Oct 18 Office Hours	Oct 19 Project Check-in I
Oct 20	Oct 21 Assignment 5 Due	Oct 22 Lecture 13 Assignment 6	Oct 23	Oct 24	Oct 25 Office Hours	Oct 26
Oct 27	Oct 28 Assignment 6 Due	Oct 29 Assignment 7	Oct 30 Office Hours	Oct 31 No make-up lecture scheduled.	Nov 1	Nov 2
Nov 3	Nov 4 Assignment 7 Due	Nov 5 Lecture 14 Assignment 8	Nov 6	Nov 7 Lecture 15	Nov 8 Office Hours	Nov 9 Project Check-in II Appraisal II
Nov 10	Nov 11 Assignment 8 Due	Nov 12 Lecture 16 Assignment 9	Nov 13	Nov 14 Lecture 17	Nov 15 Office Hours	Nov 16
Nov 17	Nov 18 Assignment 9 Due	Nov 19 Lecture 18 Assignment 10	Nov 20 Project Submission	Nov 21 Lecture 19	Nov 22 Office Hours	Nov 23
Nov 24	Nov 25 Assignment 10 Due	Nov 26 Lecture 20	Nov 27	Nov 28 Project Presentations*	Nov 29 Office Hours	Nov 30
Dec 1	Dec 2	Dec 3	Dec 4 Reading Week	Dec 5	Dec 6 Office Hours	Dec 7 Course Reflection
Dec 8	Dec 9	Dec 10	Dec 11 Final Exam Exam Week	Dec 12	Dec 13	Dec 14

* Attendance is required for this class
^† Due date may be extended by one day.
^‡ Lecture may be repeated upon request.